Authors’ Seminars recordings available on our Vimeo page

IEEE J-MMCT has just received an Impact Factor (IF)! Many thanks to our community of authors, reviewers, readers and editorial team members. All of JMMCT’s metrics (downloads/citations per paper, Scopus CiteScore=3.7) are trending upwards and hopefully this will also be the case for the journal’s new IF, moving forward.

Lorentz-Invariant Meshless Vector Basis Function for Translational Motion of Coordinates in Computational Electromagnetics

Authors: Arman Afsari; Paulo de Souza; Amin Abbosh; Yahya Rahmat-Samii

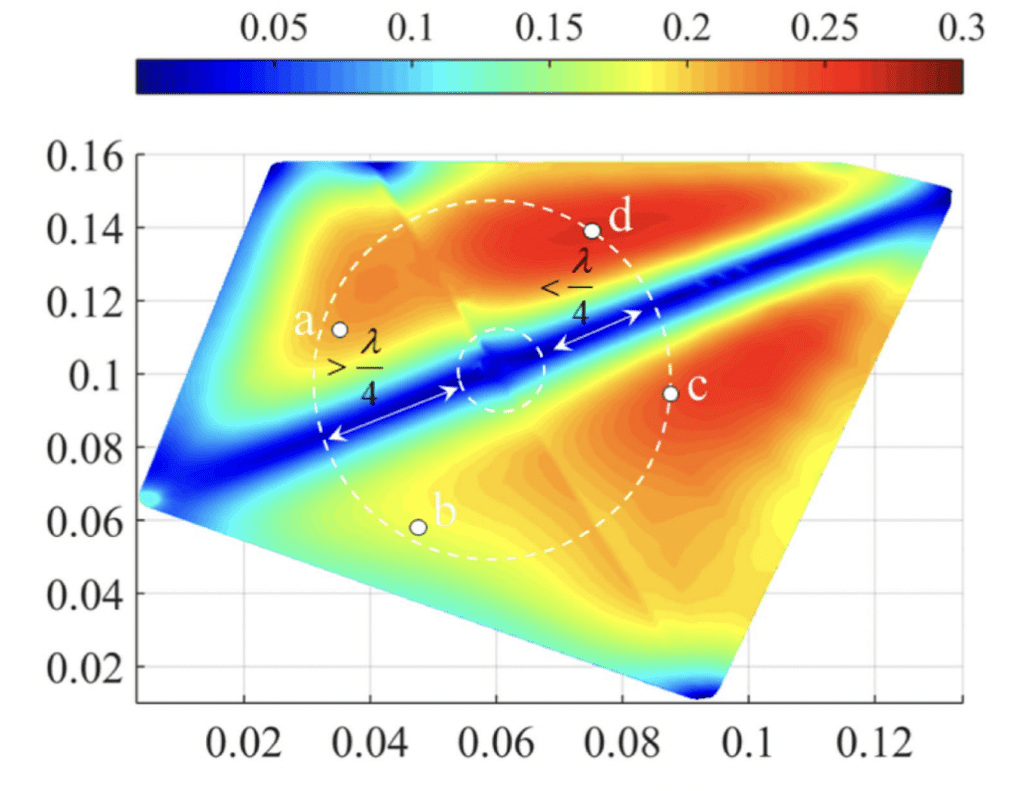
Laws of physics remain unchanged under translational motion of coordinates. To guarantee the above postulate in electromagnetics, Lorenz gauge eliminates the additional terms generated in the wave equation of magnetic vector potential during translational motion. When it comes to computational electromagnetics, nonetheless, Coulomb gauge is still preferred to represent the divergence of the magnetic vector potential; the vector basis functions involved in the computation of magnetic vector potential are thus divergence-free. There is, however, an immediate consequence that we shall consider here. These vector basis functions cannot incorporate any kinematic transformation of the system of coordinates. The solution achieved by them is, therefore, invalid under translational motion of the system of coordinates as a whole. Less attention has been paid to this side of computational electromagnetics, as the problems that we solve do not usually undergo any kinematic transformation. The new meshless vector basis function presented in this article is Lorentz-invariant. The solution achieved by it is, therefore, valid under translational motion. Even in local problems, the solution achieved by the newly-introduced Lorentz-invariant vector basis function demonstrates more accuracy and efficiency with respect to the solution achieved by the divergence-free vector basis functions in meshless method.

DOI: 10.1109/JMMCT.2023.3303813

Method of Characteristic Modes Analysis and Manipulation for Antenna Design by Using Generalized Partial Element Equivalent Circuit

Authors: Yuhang Dou; Hao Chen

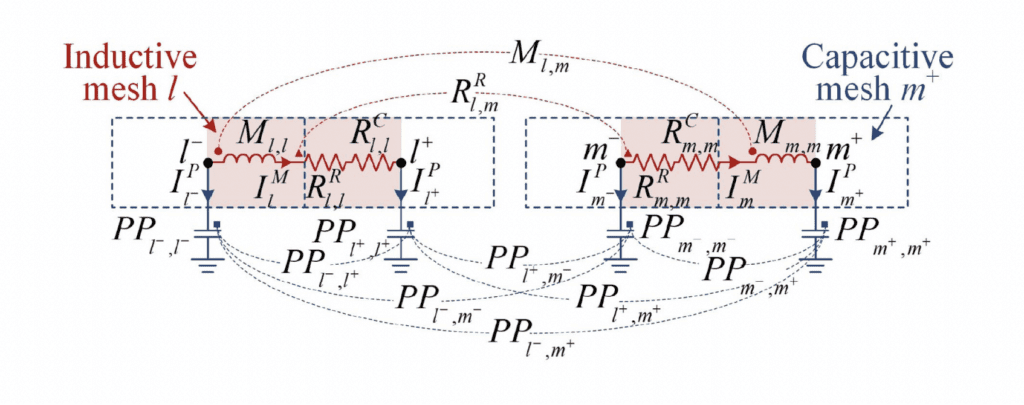
A method of analyzing characteristic modes (CMs) of antennas with multiple lumped LC loads is proposed based on the full-wave generalized partial element equivalent circuit (GPEEC) model. With the GPEEC model, a comprehensive analysis of antennas can be achieved simultaneously, including but not limited to simulating time-/frequency-domain responses, evaluating radiation efficiency contributed by the self- and mutual radiated power separately, and plotting current and field distribution. Three design examples are demonstrated, including analyzing the working mechanism of the self-curing decoupling technique for mobile terminals from the view of CMs, extending the bandwidth of an antenna in LTE-A low-frequency bands, and creating a pair of MIMO antennas in the low LTE-A bands. These examples are verified theoretically and experimentally, showing the high potential of this method in analyzing and designing antennas for mobile terminals.

DOI: 10.1109/JMMCT.2023.3242714

A TF/SF Plane Wave Source Condition for the Constraint-Preserving FVTD Method

Authors: Kaiser Niknam; Jamesina J. Simpson

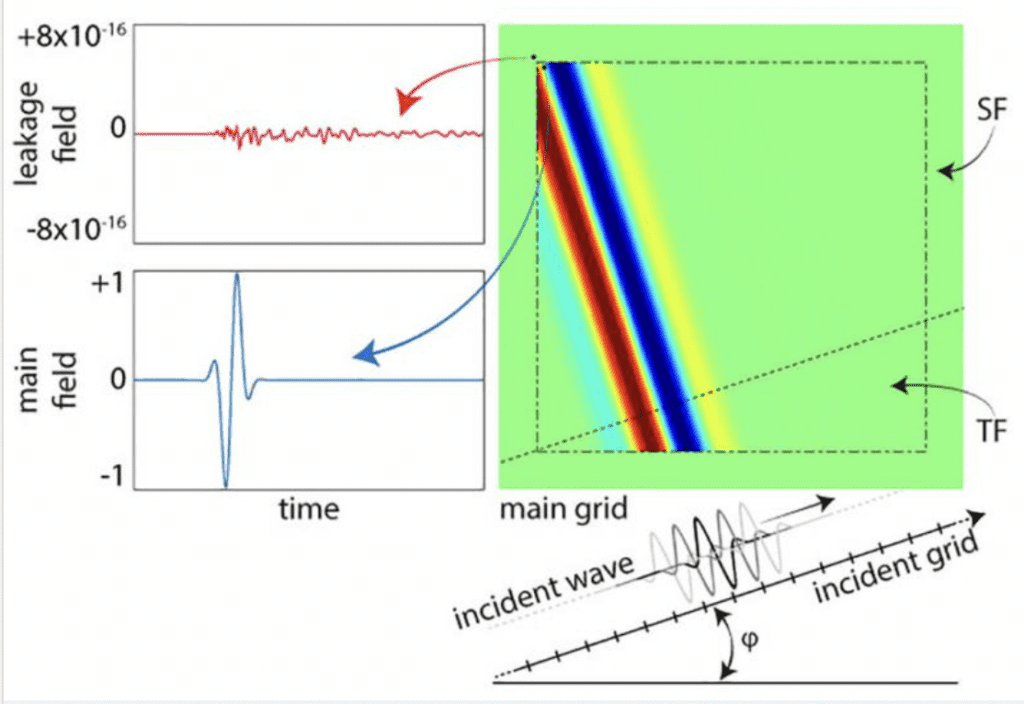
A low-leakage total-field/scattered-field plane wave source condition capable of propagating at any incident angle is developed for a newly-developed DGTD-based FVTD method. This constraint-preserving FVTD method provides solutions up to any order of accuracy, preserves the divergence constraints imposed by Gauss’ laws, and may be easily adapted to non-conformal and unstructured meshes. In order to implement the proposed plane wave source condition, several of the steps within the updating loop of the FVTD model, including the Riemann solvers and update equations, must be adapted to ensure the field variables always remain consistent (are consistently designated as either total or scattered fields). The proposed total-field/scattered-field technique is shown to provide numerical leakage errors at the level of machine precision (−300 dB) for second-, third-, and fourth-order constraint-preserving FVTD schemes.

DOI: 10.1109/JMMCT.2023.3241190

Predicting Output Responses of Nonlinear Dynamical Systems With Parametrized Inputs Using LSTM

Author: Lihong Feng

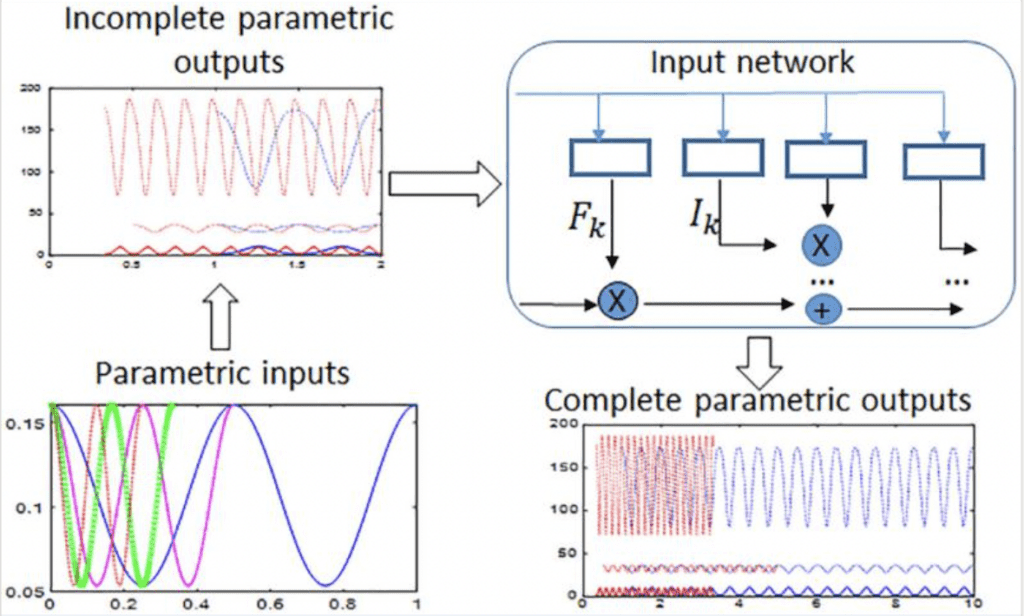
Long Short-Term Memory (LSTM) has been more and more used to predict time evolution of dynamics for many problems, especially the fluid dynamics. Usually, it is applied to the latent space after dimension reduction of the full dynamical system by proper orthogonal decomposition (POD), autoencoder (AE) or convolutional autoencoder (CAE). In this work, a proposal to directly apply LSTM to the data of the output without dimension reduction for output response prediction is made. Based on the standard LSTM structure, a LSTM network is proposed with modified activation functions which is shown to be much more robust for predicting periodic waveforms.

DOI: 10.1109/JMMCT.2023.3242044

A Systematic Approach to Adaptive Mesh Refinement for Computational Electrodynamics

Authors: Dinshaw S. Balsara; Costas D. Sarris

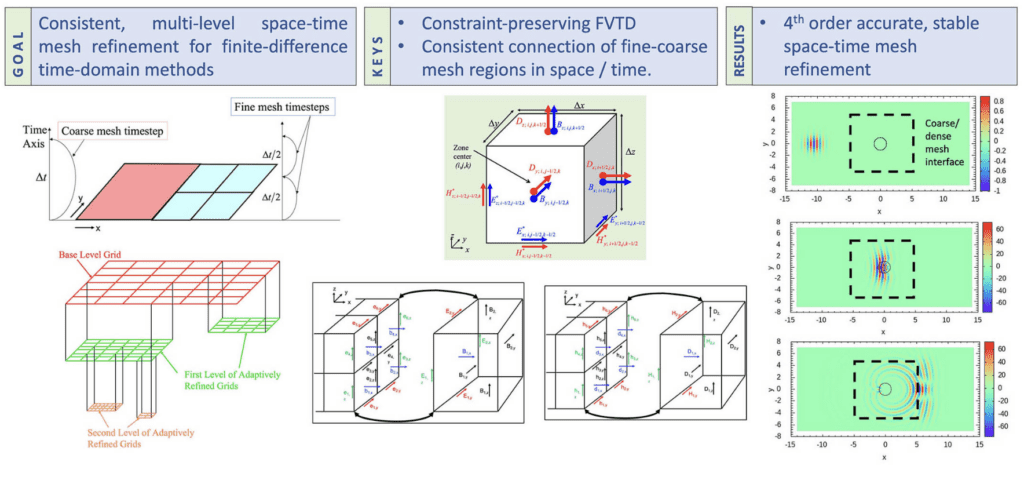
There is a great need to solve CED problems on adaptive meshes; referred to here as AMR-CED. In this paper, a new class of AMR-CED methods are presented that are free of “long-term instability” because they are based on a more careful understanding of the constraints in Maxwell’s equations and their preservation on a single control volume. The important building blocks of these new methods are: 1) Timestep sub-cycling of finer child meshes relative to parent meshes. 2) Restriction of fine mesh facial data to coarser meshes when the two meshes are synchronized in time. 3) Divergence constraint-preserving prolongation of the coarse mesh solution to newly built fine meshes or to the ghost zones of pre-existing fine meshes. 4) Electric and magnetic field intensity-correction strategy at fine-coarse interfaces.

DOI: 10.1109/JMMCT.2022.3233944

Spontaneous Emission Rate and the Density of States Inside a One Dimensional Photonic Crystal

Author: Ebrahim Forati

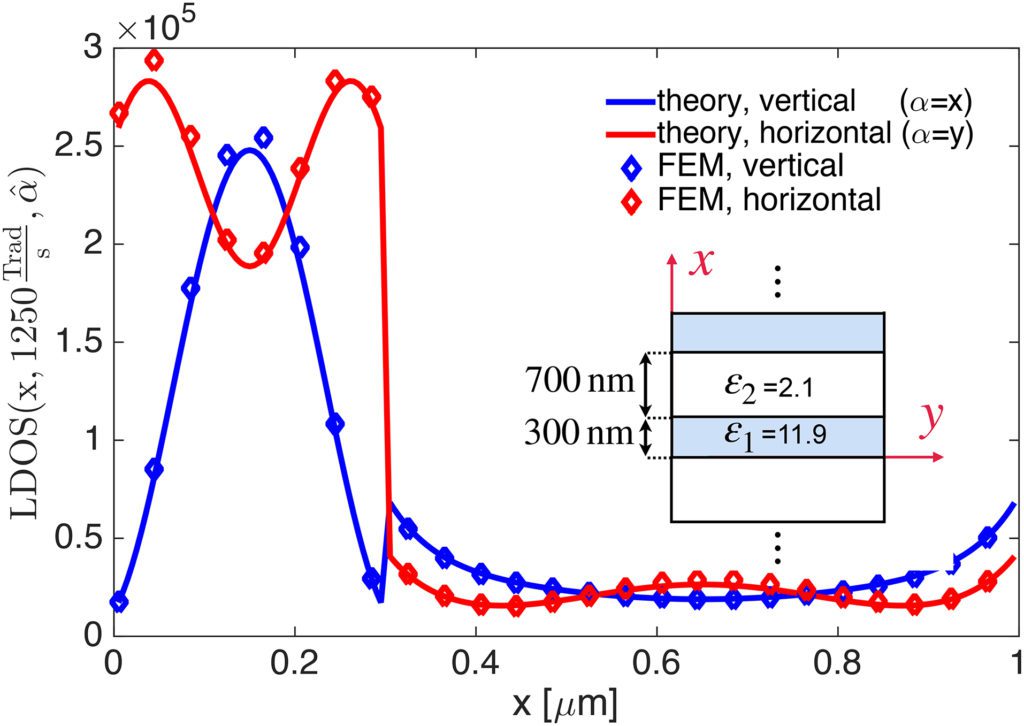
Different densities of electromagnetic states inside a one dimensional photonic crystal (1D PC) are studied. Hertz vector formalism is used to calculate Green’s tensor inside a layered structure, semi-analytically. Based on the obtained Green’s tensor, the local density of electromagnetic states (LDOS) and the density of states (DOS) inside a 1D PC are calculated and discussed. The Green’s tensor is also used to approximate the density of Bloch states inside the 1D PC and is compared with its exact calculation based on the 1D PC dispersion relations. Using a practical 1D PC parameters in the visible range, the aforementioned quantities are calculated and verified with a full-wave solver based on finite element method (FEM). The formulations and the results are aimed to be helpful in thermal and spontaneous radiation studies.

DOI: 10.1109/JMMCT.2022.3153405

Analysis of Sound Propagation Across Acoustic Ducts With Discontinuities Using a High Precision Finite Element Method

Authors: Chaoxian Qi; Shubin Zeng; Jiefu Chen

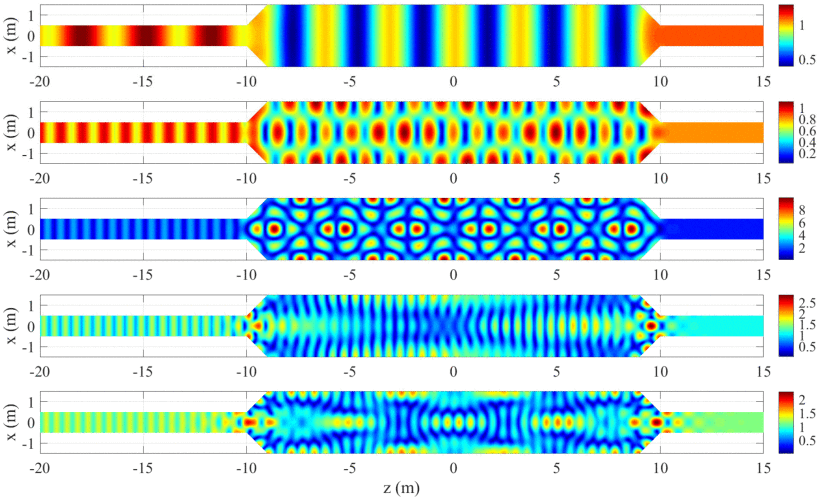
A high-precision numerical method is presented to model acoustic wave propagation along a duct with discontinuities. The discontinuous duct can be divided into homogeneous and inhomogeneous substructures. The inhomogeneous substructures are purely discretized by the conventional finite element method, while only cross-sectional areas need to be discretized for homogeneous substructures. The Legendre transformation is then used to transform the semi-discretized problem from the Lagrangian system into the Hamiltonian system. A Riccati equation-based high precision integration method is taken to perform the integral along the longitudinal direction, i.e., the homogeneous direction, to generate stiffness matrices of substructures. The final system stiffness matrix is obtained by assembling stiffness matrices of homogeneous substructures with stiffness matrices of inhomogeneous substructures. Numerical examples are provided to validate the proposed method, and these examples have shown high efficiency and accuracy compared with the conventional finite element method.

DOI: 10.1109/JMMCT.2022.3154409

Applying Loop-Star Functions With Multibranch Rao-Wilton-Glisson Basis Functions in the Time Domain Electric Field Integral Equation

Authors: Yuyang Hu; Gaobiao Xiao; Shifeng Huang; Rui Liu

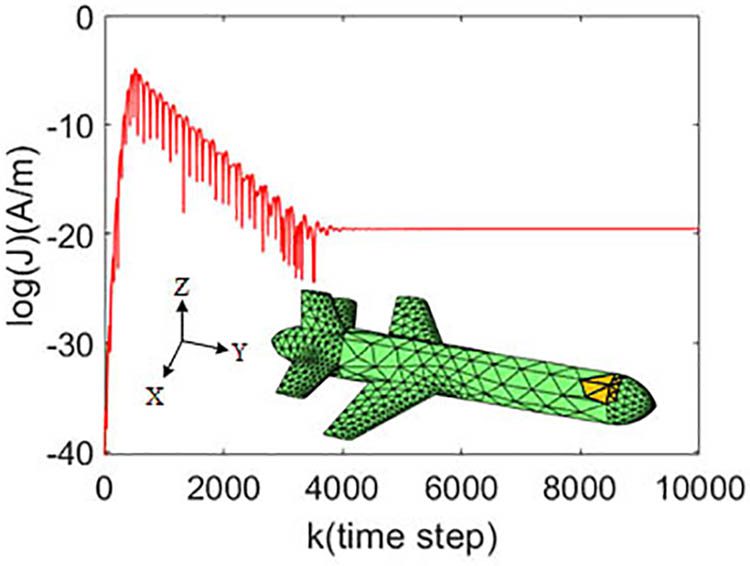
In this paper, novel loop-star basis functions with the multibranch Rao-Wilton-Glisson (MB-RWG) basis functions are applied to obtain the low-frequency stable solution of the time domain electric field integral equation (TD-EFIE). With the help of the MB-RWG basis functions, it is possible to realize the quasi-Helmholtz decomposition in the time domain between different regions that are discretized separately with nonconformal meshes, by modifying slightly the generation of the loop and star bases at the interfaces. Especially, the temporally differentiated form of the TD-EFIE is tested by the star basis, while the undifferentiated form of the TD-EFIE is tested by the loop basis. By means of the filtering technique, the components of the solution which have the potential of growing exponentially have been treated. Numerical results illustrate the accuracy and robustness of the proposed method in analyzing the transient scattering problems of perfectly electrical conducting (PEC) objects.

DOI: 10.1109/JMMCT.2022.3152400

Simulation of Surface Enhanced Raman Scattering From Nanoparticles With Wideband Nested Equivalence Source Approximation

Authors: Mengmeng Li; Yanmeng Hu

Surface Enhanced Raman Scattering (SERS) has been widely used in the fields of surface science, spectral analysis, biosensors, and biomedical detection. A wideband nested equivalent source approximation (WNESA) accelerated method of moments (MoM) of multiple material regions is proposed, for the analysis of SERS by nanostructure. The SERS affected by the diameter and distance between gold nanospheres for dimer structure is studied through numerical simulations with WNESA. It is found that nanoparticles-based SERS substrates with different dimensions and distances will produce different excitation wavelengths and SERS enhancement factors, by evaluating the variation of hot spot positions with wavelengths. The computational complexity of WNESA for SERS substrate simulation is O ( N log N ), where N is the number of unknowns. Significant improvement of the design efficiency of nanostructures for increasing the magnitude of SERS can be achieved.

DOI: 10.1109/JMMCT.2022.3147232

Manifold Harmonics and Their Application to Computational Electromagnetics

Authors: A. M. A. Alsnayyan; L. Kempel; B. Shanker

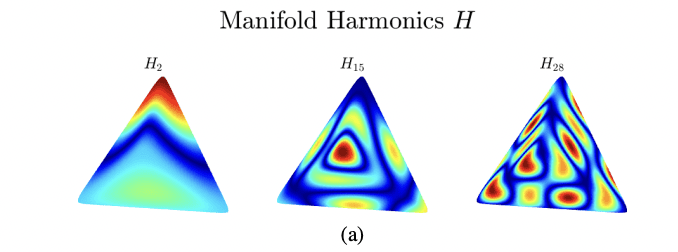
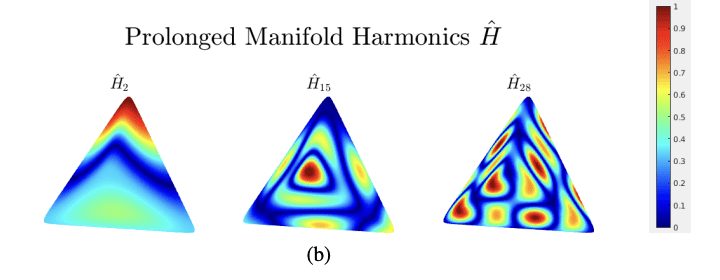
The eigenfunctions of the Laplace-Beltrami operator (LBO), or manifold harmonic basis (MHB), have many applications in mathematical physics, differential geometry, machine learning, and topological data analysis. MHB allows us to associate a frequency spectrum to a function on a manifold, analogous to the Fourier decomposition. This insight can be used to build a framework for analysis. The purpose of this paper is to review and illustrate such possibilities for computational electromagnetics as well as chart a potential path forward. To this end, we introduce three features of MHB: (a) enrichment for analysis of multiply connected domains, (b) local enrichment (L-MHB) and (c) hierarchical MHB (H-MHB) for reuse of data from coarser to fine geometry discretizations. Several results highlighting the efficacy of these methods are presented.

DOI: 10.1109/JMMCT.2022.3199612

EM Scattering by Core-Shell Gyroelectric-Isotropic and Isotropic-Gyroelectric BoRs using the EBCM

Authors: Grigorios Zouros; Georgios D. Kolezas; Konstantinos Katsinos

We employ the extended boundary condition method (EBCM) and construct a solution for the problem of electromagnetic (EM) scattering by anisotropic core-shell bodies of revolution (BoRs). In particular, two different core-shell configurations are examined: the gyroelectric-isotropic and the isotropic-gyroelectric setup. To construct the solution, we employ two groups of integral representations (IRs)—one group for each configuration solved—in conjunction with the discrete eigenfunction (DE) expansion of the fields in terms of spherical vector wave functions (SVWFs) for the gyroelectric regions. We demonstrate the validity and the computational performance of the method by comparisons with the HFSS commercial software for various core-shell setups such as spheroidal, cylindrical and combined spherical-cylindrical BoRs. We also employ ADDA, a particular version of the discrete dipole approximation (DDA) method, to trace the boundaries of validity of the EBCM. Finally, we present an application of the method to the study of magnetically-tunable spheroidal THz antennas. The method can be used in a variety of potential EM applications including microwaves, functional photonics structures, as well as nanoantenna engineering.

DOI: 10.1109/JMMCT.2022.3176245

Computing Eigenvalues of Dielectric Waveguides by a Method of Auxiliary Sources with Two Excitation Sources

Authors: Minas Kouroublakis; Nikolaos Tsitsas; George Fikioris

The Method of Auxiliary Sources with an Excitation Source (MAS-ES) has been successfully employed to compute the eigenvalues of arbitrarily-shaped hollow waveguides with perfectly electric conducting walls. The main advantages of this method are its simplicity, and that it is free of spurious eigenvalues, in contrast to the standard MAS approach. In this paper, we demonstrate that the MAS-ES is also effective in computing the propagation constants β of a cylindrical dielectric waveguide. It is emphasized that two excitation sources are required to excite hybrid modes of the dielectric waveguide. The modified method is named MAS with Two Excitation Sources (MAS-TES). The fact that the propagating modes are localized in the vicinity of the core allows us to determine the eigenvalues by measuring the response of the core to the excitation sources. This is performed by employing a response function F(β) which is maximized when a standing wave is formed in the core. Plotting F(β) for a dense set of β results in a response curve the peaks of which correspond to the waveguide’s eigenvalues. The method is tested for several dielectric waveguides’ geometries, including two multimode cases, and it is shown that it is free from discrete and continuous spurious solutions. All the MAS-TES results are compared with those obtained by a FEM-based commercial software and an excellent agreement is exhibited.

DOI: 10.1109/JMMCT.2022.3176203

Full-Wave Methodology to Compute the Spontaneous Emission Rate of a Transmon Qubit

Authors: Thomas E. Roth; Weng C. Chew

The spontaneous emission rate (SER) is an important figure of merit for any quantum bit (qubit), as it can play a significant role in the control and decoherence of the qubit. As a result, accurately characterizing the SER for practical devices is an important step in the design of quantum information processing devices. Here, we specifically focus on the experimentally popular platform of a transmon qubit, which is a kind of superconducting circuit qubit. Despite the importance of understanding the SER of these qubits, it is often determined using approximate circuit models or is inferred from measurements on a fabricated device. To improve the accuracy of predictions in the design process, it is better to use full-wave numerical methods that can make a minimal number of approximations in the description of practical systems. In this work, we show how this can be done with a recently developed field-based description of transmon qubits coupled to an electromagnetic environment. We validate our model by computing the SER for devices similar to those found in the literature that have been well-characterized experimentally. We further cross-validate our results by comparing them to simplified lumped element circuit and transmission line models as appropriate.

DOI: 10.1109/JMMCT.2022.3169460

Exact Solution of New Magnetic Current Based Surface-Volume-Surface EFIE and Analysis of Its Spectral Properties

Authors: Osman Goni; Vladimir I. Okhmatovski

A novel magnetic current based Surface-Volume-Surface Electric Field Integral Equation (SVS-EFIE-M) is presented for the problem of scattering on homogeneous non-magnetic dielectric objects. The exact Galerkin Method of Moments (MoM) utilizing both the rotational and irrotational vector spherical harmonics as orthogonal basis and test functions according to the Helmholtz decomposition is implemented to solve SVS-EFIE-M analytically for the case of dielectric sphere excited by an electric dipole. The field throughout the sphere is evaluated and compared against the exact classical Mie series solution. The two are shown to agree to 12 digits of accuracy upon a sufficient number of basis/test functions taken in the MoM solution and the Mie series expansion. This exact solution validates the rigorous nature of the new SVS-EFIE-M formulation. It also reveals the spectral properties of its individual operators, their products and their linear combination. The spectrum of the MoM impedance matrix is also obtained. It is shown that upon choosing basis and test functions in L2(S) space and evaluating testing inner products in the same space, the MoM impedance matrix features bounded condition number with increasing order of discretization and/or at low frequencies. This makes the proposed SVS-EFIE-M formulation free of oversampling and low-frequency breakdowns giving it advantage both over its SVS-EFIE-J predecessor and classical double-source integral equations such as PMCHWT, Muller, and others suffering from this type of numerical instabilities inherent to their inferior spectral properties

DOI: 10.1109/JMMCT.2022.3164942

3-D Steady Heat Conduction Solver via Deep Learning
Authors: Yinpeng Wang; Jianmei Zhou; Qiang Ren; Yaoyao Li; Donglin Su

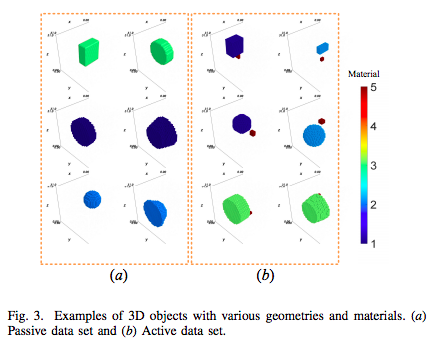
Conventional numerical heat conduction solvers are exceedingly computationally expensive and memory demanding. Recent advances in deep learning have witnessed its extensive application in computational physics field. Compared to traditional methods, deep learning framework emerges superior computational efficiency, providing a substitution for speeding up the calculation. In this paper, we propose an innovate deep learning framework to predict the 3D temperature field in a cubic region filled with random objects of various geometries and materials. The framework is capable of resolving both passive and active heat conduction problems. After being fully trained, it can achieve similar precision to the finite element method (FEM), while the calculation speed is accelerated by two orders of magnitude. Furthermore, the deep learning model has demonstrated robust generalization ability in predicting the temperature distribution of the cases with real-world objects not existing in the data set. We believe that the framework paves the way for solving complex heat conduction problems in engineering, as well as inverse problems in the future.

DOI: 10.1109/JMMCT.2021.3106539

Space-time Adaptive Processing Concept for Calculation Speed Improvement In Multi-Region/FDTD Method

Authors: Kei Asahi ; Takuji Arima ; Akihisa Uematsu ; Toshiyuki Nishibori ; Toru Uno

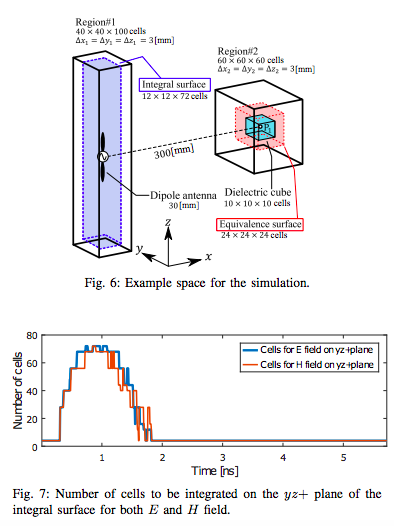
Nowadays, the demand for large-scale electromagnetic simulations has been generally increasing, and the FDTD method is one of the effective electromagnetic simulation methods. The MR (Multi-Region) / FDTD method allows the calculation of free space between the antenna and the objects to be omitted from the simulation model. This method utilizes the equivalence theorem to connect the multiple regions. One of the limitations of the MR/FDTD method is a high time complexity when it involves large-scale simulations. Thus, in this communication, we propose a space-time adaptive processing concept to optimize the computation time of the MR/FDTD method. In the proposed method, a quadtree structure is utilized for adaptive processing. We confirmed the effectiveness of the proposed method using numerical simulations.

Reverse-Time Migration by Combining Laplacian Filtering with Wavefield Decomposition for High-Resolution Subsurface Imaging

Authors: Xinrong Mao ; Yuanguo Zhou ; Fei Lei ; Lushun Zhao ; Kirill Zeyde

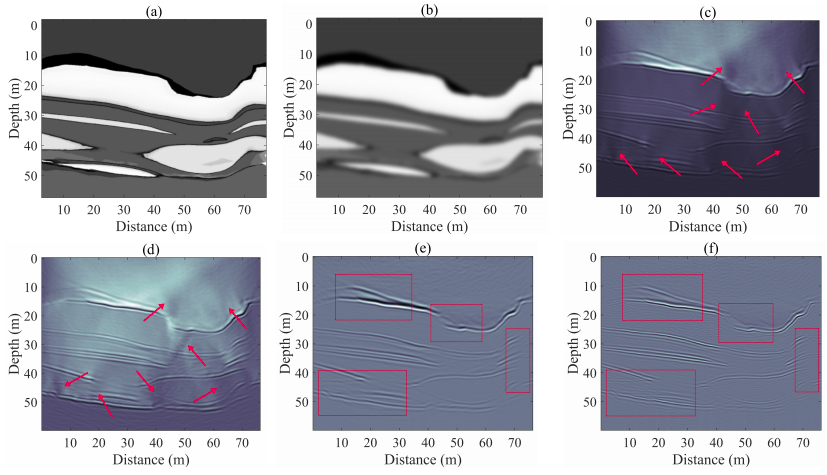
Reverse-time migration (RTM) is considered to be one of the most accurate migration methods, especially for imaging geologically complex structures. Howeverthe conventional RTM using cross-correlation imaging condition is subject to strong migration artifacts. Recent researches on electromagnetic wavefield decomposition exhibit that the method can greatly suppresses the internal reflection noise, however, it is still subject to residual noise. To further eliminate the low-frequency noise to obtain high-resolution subsurface image, a novel electromagnetic imaging scheme by combining a Laplacian filtering with wavefield decomposition is presented, and the pseudospectral time-domain (PSTD) method is introduced to solve the time-dependent partial differential equations efficiently. In this work, we apply the Laplacian filtering on each wavefield snapshot in space domain to sharpen the field distribution. The filtered wavefields are further decomposed into downgoing and upgoing components for final imaging. Numerical experiments show that the proposed method balances the amplitudes of reflectors, and exhibits higher resolution compared to the conventional RTM.

DOI: 10.1109/JMMCT.2021.3086833

Potential-Based Time Domain Integral Equations Free from Interior Resonances

Authors: Thomas Edgar Roth ; Weng Cho Chew

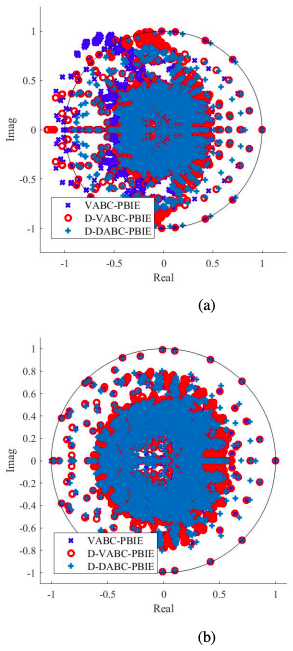
Potential-based integral equations are being explored to develop numerical methods that avoid low-frequency breakdown issues so that they can analyze multiscale structures that are becoming increasingly important in electromagnetic engineering. This work continues the development of potential-based time domain integral equations by presenting three new formulations in the Lorenz gauge that do not support interior resonances. These modifications allow the methods to be applied to deeply multiscale structures of practical importance that contain significantly subwavelength- and wavelength-sized geometric features. Appropriate marching-on-in-time discretization schemes are developed for each formulation that fully conform to the temporal Sobolev space properties of the integral equations. It is shown that following this approach leads to a discrete system with improved stability properties. Further, it is demonstrated that this new system can produce accurate results over broad bandwidths and analyze deeply multiscale systems that previous potential-based time domain integral equations could not.

DOI: 10.1109/JMMCT.2021.3086622

CNN for Compressibility to Permittivity Mapping for Combined Ultrasound-Microwave Breast Imaging

Authors: Pedram Mojabi ; Max Hughson ; Vahab Khoshdel ; Ian Jeffrey ; Joe Lovetri

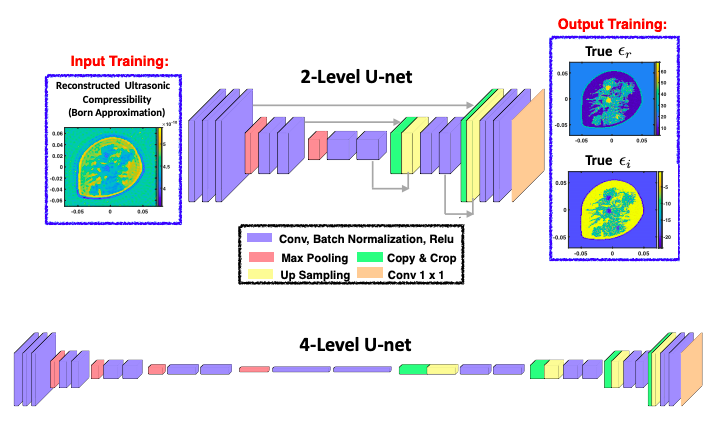
Combined ultrasound-microwave breast imaging requires a mechanism to guide one imaging modality using the other. To this end, a convolutional neural network (CNN) is proposed for the mapping of ultrasound property images to dielectric property images for combined ultrasound-microwave breast imaging applications. In this approach, higher resolution ultrasound images are obtained by inverting the ultrasound scattered pressure data using a linearized inverse scattering algorithm. The reconstructed Born-based ultrasound compressibility images are then used to predict dielectric images for the same breast phantoms. These predicted dielectric images can then be used to guide microwave imaging reconstruction to achieve higher accuracy images. To this end, a CNN is trained based on the input of the reconstructed quantitative ultrasonic compressibility and the output of the true quantitative dielectric properties corresponding to the same numerical phantom. Several numerical MRI-derived breast phantoms are used to train and test this CNN. The predicted dielectric properties are tested using different numerical MRI-derived breast phantoms and the predicted profiles show promising results. The predicted dielectric properties are also used as the initial guess prior for the microwave inversion algorithm which leads to the enhancement of the reconstruction of dielectric properties as compared to the blind microwave inversion.

DOI: 10.1109/JMMCT.2021.3076827

A call for papers for our annual special section on the 2020 IEEE International Conference on Computational Electromagnetics (ICCEM 2020) is available. Expected online publication date is December 2020.

I am profoundly honoured by and excited for the opportunity to serve as the Editor-in-Chief of the IEEE J. on Multiscale and Multiphysics Computational Techniques for the next three years.

This journal is very young, but highly aspiring; its objective is to report significant new developments in the theory and applications of computational techniques for problems of interest across its three founding IEEE societies, the Antennas and Propagation, Electromagnetic Compatibility and Microwave Theory and Techniques Society, and beyond: to researchers and practitioners in other areas of science and engineering, working on subjects related to electromagnetic fields.

Many new areas of research in natural sciences and engineering evolve on and across rather than within conventional disciplinary boundaries. Research on computational electromagnetics methods will be likewise advancing on these boundaries, coupling Maxwell’s equations with mechanical, thermal, chemical and quantum phenomena solvers. Moreover, translating our detailed knowledge of component parts to their impact on the behavior of the systems they belong to, defines the frontier of multiscale modeling, where potentially heterogeneous models are integrated over the wide range of spatial and temporal scales present in most physical problems.

This journal is committed to keeping up with these advances, becoming the main source of reference for the latest, high impact research on multiscale and multiphysics computations of electromagnetic fields. We will do so through our regular papers, but also with invited papers and special issues on emerging areas of computational techniques. Our journal will also solicit and welcome contributions from researchers in any area of computational science and engineering on techniques that have potential applications in electromagnetics.

Founded by three IEEE societies, this Journal ultimately belongs to you: its readers. The Associate Editors and I welcome your thoughts and suggestions on the future of the Journal. For all of us, J-MMCT’s journey continues, with a sense of optimism and responsibility.

Costas Sarris, Editor-in-Chief